Continuing our primer series, we now turn to public key cryptography, an essential element of DLTs which is used to ensure security, authenticity and integrity. This piece will look at the history of symmetric and asymmetric key algorithms, before turning to detail how they work, how they are used and how Radix uses them specifically.
A brief history of cryptography
Cryptography was for centuries limited to symmetric key algorithms. A symmetric key algorithm is where there is one key which both locks and unlocks access. For the purpose of this article, a key refers less to a physical object and more to any mechanism for locking/unlocking. As such one of the more famous early examples of cryptography, Caesar’s Cipher, saw the key become the amount of letters needed to shift over in the alphabet for the message to make sense e.g. if the message was FDW then with a left shift of 3 we could decipher it as CAT.
This symmetric standard persisted until the 1970s, when two GCHQ employed British cryptographers known as James H. Ellis and Clifford Cocks proposed public key cryptography, although it was suppressed due to its classified nature until 1997.
This was subsequently followed by the Diffie-Hellman key exchange, developed by Whitfield Diffie and Martin Hellman, although Malcolm J. Williamson (another GCHQ employee whose work was not released to the public until decades later) had also previously independently developed the same technique. The Diffie-Hellman key exchange was one of the first publicised examples of a public key exchange and would be closely followed less than two years later by a practical public-key encryption scheme developed by Rivest, Shamir and Adleman’s that would be known as RSA and would become synonymous with public-key encryption.
These developments were then followed by the independently developed work of Koblitz and Miller, which saw the introduction of elliptic curve cryptography (ECC). This allowed for smaller keys whilst maintaining equivalent levels of security, essentially making ECC more secure than prior algorithms.
This body of work is the foundation of DLT public-key cryptography.
How does it work?
DLTs would not function with symmetric key algorithms, for obvious reasons. Bitcoin was created in order to allow two parties to trust each other without the need to trust a third party. If the key is the same for both locking and unlocking, then if Alice wished to send some BTC to Bob she would have to trust that Bob would not unlock her account and steal everything.
This is unworkable.Asymmetric key algorithms, however, provide two keys – a public and a private key. This means that Bob can provide his public key to Alice to receive BTC safe in the knowledge that she will not be able to unlock his account – that is what Bob’s private key is for. Furthermore, if Alice wanted to send information to Bob and Bob wanted to make sure the information was really coming from Alice, then Alice could give her public key to Bob. She can then sign messages using her private key, which Bob is then able to verify using her public key.
For this to be a safe and efficient method of transaction:
- No-one can be able to find out the private key despite having access to the public key
- It is easy to create the public key when the private key is known
These are known as the one-way and trapdoor functions respectively. The difference between the two is that a trapdoor function is reversible, whereas a one-way function is (as the name suggests) not. These functions are enabled by two types of solutions – the factorization of large numbers and the discrete logarithm problem.
Cryptography implementations such as RSA work on the basis that it is extremely difficult and time consuming to factor large numbers. An incentivized RSA challenge began in 1991, yet of the more than 50 numbers laid out, just 20 (with the smallest decimal digits) have been solved to date, highlighting the computational resources required to crack encryption relying on large number factorization.
The trapdoor function of ECC, however, rests on what is known as the discrete logarithm problem rather than factoring large numbers. The discrete logarithm problem is, given the same length of inputs, harder to solve than factorization, and this is what allows ECC to maintain the same levels of security as prior solutions whilst using smaller keys. A more detailed look at ECC and the discrete logarithm problem can be found here.
Both the factorization of large numbers and the discrete logarithm problem are fundamental to public key cryptography. They are what enable us to use public keys without worrying that a malicious actor will be able to find out private key based on said public key.
What are they used for?
This public key cryptography enables DLTs to achieve a number of things including:
- Authenticity: When Alice uses her private key to sign a Bitcoin transaction, the recipient knows that it has come from her and her alone
- Confidentiality: Information encrypted with Alice’s public key can only be decrypted by using her private key – meaning that no-one can access Alice’s wallet bar her
- Non-repudiation: If Alice signs and sends a message, she can not claim at a later date that she did not send it
These points rest upon the assumption that Alice has not lost or had her private key stolen.
How are they used in Radix
The Radix ledger and clients use elliptic curve public key cryptography primarily for:
- Signing content
- Encrypting content
Signing content
Signatures are created by computing a hash function over the input data to be signed. This hash is then encrypted using the signer’s private key.
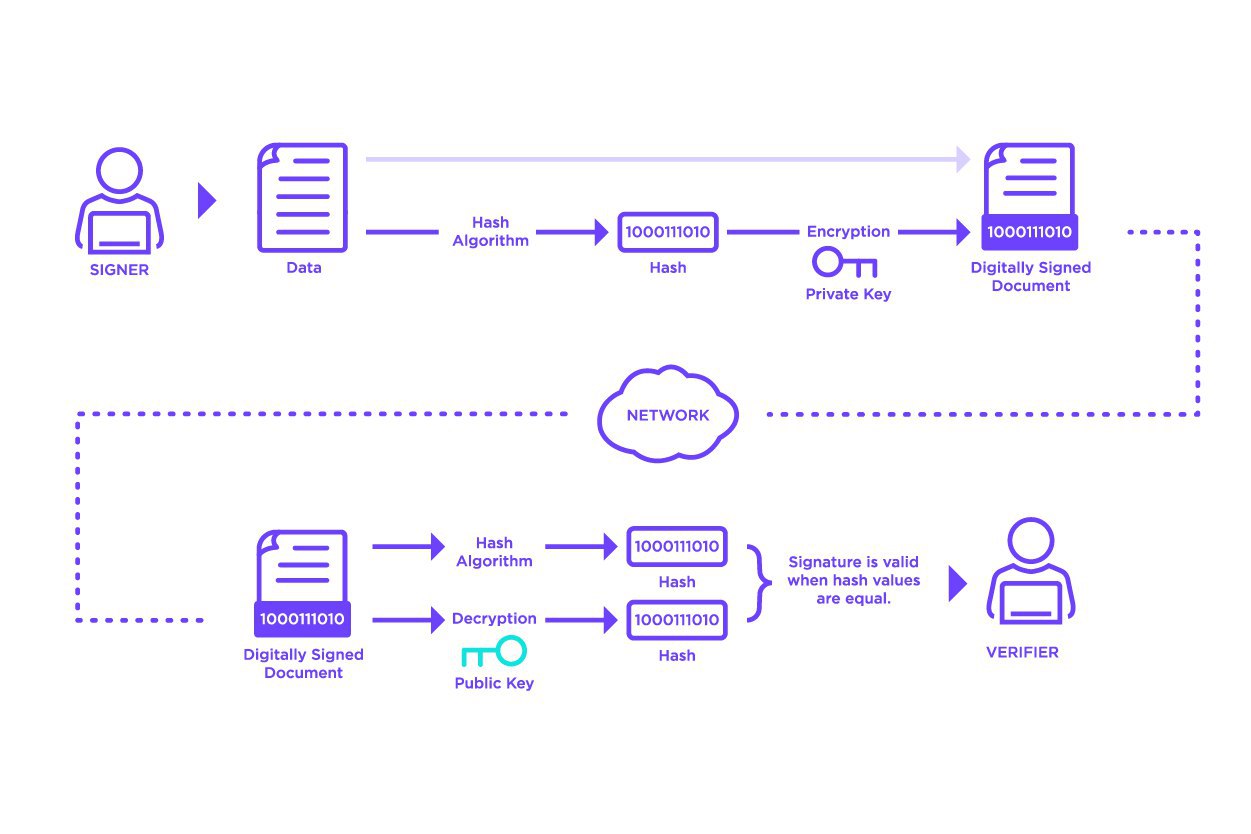
Anyone wishing to validate the signature can compute the same hash over the input data and can also decrypt the encrypted hash using the signer’s public key. The computed hash and decrypted hash can be compared, and if equal, the verifier can be confident that, because of the properties of hash functions, the input data has not changed and, because of the properties of public-key cryptography, that the signer did actually sign the data.
Signatures provide the basis for two key requirements of a ledger: authentication and non-repudiation. The properties of public-key cryptography and hash functions provide a very high degree of confidence that no other actor can produce a valid signature for a given piece of input data. Because of this, we can be confident that signed data on the ledger has indeed been signed by the signer and is authentic and non-repudiable.
Hash functions have been discussed in a previous post “What are hashes and hash functions?”.
Encrypting content
In some cases, someone using the Radix ledger, for example Bob, may prefer to communicate with Alice in a way that means that only Alice has access to the data. In this case, Bob can encrypt data with Alice’s public key — because of the properties of public-key cryptography, Bob can have a very high degree of confidence that only Alice will be able to access the unencrypted data using her private key.
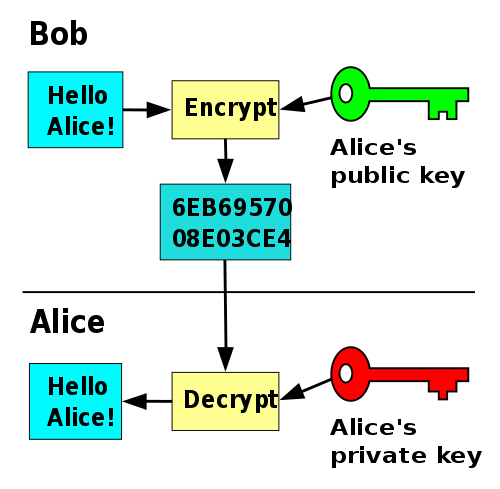
In practice, using public-key cryptography for encryption is more complicated than has been described here, as public-key algorithms typically consume too many computing resources for encrypting large amounts of data directly. Some of this will be covered in a future post on symmetric keys and session keys.



.svg)


