Two of our prior posts have looked at hashing functions and public key cryptography. These two technologies combine to allow us to use digital signatures, which themselves are a vital part of making and receiving transactions on decentralized networks.
What are digital signatures?
Digital signatures are, as the name suggests, a digital equivalent for signing transactions or messages. However, rather than the easily forged handwritten signature, digital signatures are protected through cryptography and therefore falsifying them is a far more onerous task.
Digital signatures are not solely used to prove identity to a recipient (ie that I am who I claim I am) but are also the basis through which we interact with the ledger. A common misconception is that Bitcoins move between wallets when we transact them – in reality, Bitcoin never ‘move’ but rather the private key I use unlocks access to them. For example, if I wish to send a BTC to Alice I need to be able to prove my ownership of said assets, which is what the private key provides.
Once I have then sent those BTC to Alice, then the ledger subsequently updates to reflect that it is now Alice’s private key which must be used to unlock access. As discussed in the public key cryptography post, public and private keys are linked – so although I would send the BTC to Alice’s public key, it is her private key which she would then use to access the funds.
Similarly, if I send a message and sign it with my private key, Alice could then verify the message by using my public key. She is then able to see if the data is what was originally sent, because of the use of hash functions. As detailed in the previous post, we use hashing to turn any input (which can include photos, documents or plain text) into a fixed output, usually represented by a long alphanumeric value.
If the input changes in any way, then the hash will be completely different. As such, if the information Alice receives is different in even the smallest way to the information sent, the digital signature would be incorrect and Alice would know that the message had been tampered with.
It also prevents anyone from attaching a digital signature to a different file or document. Digital signatures are only used once, because the digital signature is formed of both the private key and the original data being signed. Therefore the digital signature will be different each time, even when coming from the same account.
How are digital signatures useful?
As should be clear from the above, digital signatures are useful because they allow us to determine:
- Integrity: Because we can tell if the message was changed in between sent and received, we can determine the integrity of what is sent
- Authenticity: As opposed to handwritten or electronic signatures, digital signatures are exceedingly difficult to falsify. This means that if the sender is in sole control of their private key, they are the one sending a message
- Non-repudiation: Because of this, digital signatures mean we know the sender actually sent the message (again, assuming sole control over the private key). This is why digital signatures can be taken as legally binding in many countries
How do digital signatures work?
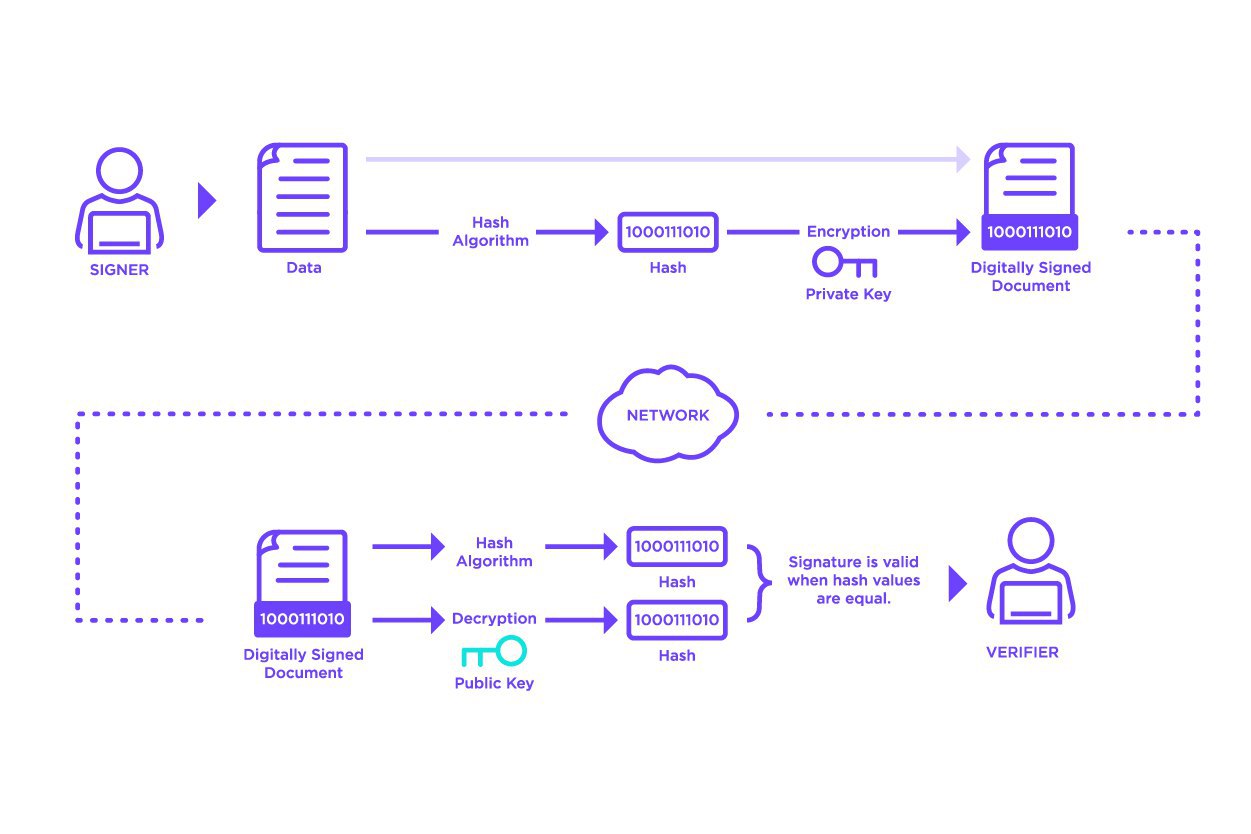
As per the above image, digital signatures work by:
- Using hash functions: The use of hash functions allows us to turn any input into a fixed size output, which both lets us easily verify it later in the process and reduces the size of the information/speeds up the process
- Use public key cryptography to encrypt hash with private key, giving the digital signature: We encrypt the hashed information with our private key
- Transmit documents and signature to recipient: The use of the private key enables the interaction from that address with the network, as it proves that the sender is the owner of the output (be it BTC or just a message)
- Recipient verifies message, computes hash of data received from sender and compares decrypted hash with computed hash: The encrypted information sent in (b) can be decrypted with the corresponding public key by the recipient. The recipient can also recalculate the hash of the included message. As per our previous discussion, if the information has been tampered with in any way then the hash would be different. If the hash is the same, then the information is what was originally sent.
This process functions because of the ‘trapdoor’ function of public key cryptography. It ensures that no-one is able to find out the sender’s private key, despite having access to their public one. This is why we can safely give out our public key to be used to decrypt data encrypted with our private one.
How are digital signatures used in Radix
The Radix ledger and clients use signatures for the purposes outlined above, to guarantee authentication, integrity and non-repudiability.For clarity, it should be noted that, like other distributed ledger systems, the Radix Ledger does not mandate any particular handling of private keys, but does require that agents holding private keys have taken sufficient steps to ensure that these keys cannot be access by unauthorised parties.
Authentication and Integrity
When a transaction is submitted to the ledger, the receiving network host will verify the signature of the transaction. If the signature verifies correctly, then this provides a great deal of assurance that both:
- The signature was signed using the signer’s private key. This assurance is possible given the properties of public-key cryptography discussed in previous posts.
- The contents of the transaction have not been modified in transit. This assurance is possible given the properties of hash functions discussed in previous posts.
Non-repudiability
As transactions are stored in the Radix ledger together with their signatures, it is possible for anyone inspecting a signed transaction to be confident that the transaction was signed with the signer’s private key. Given this, and the requirement that authorised signers retain exclusive control of their private keys, it will be difficult for the signer to dispute the transaction.



.svg)


